Conoce el módelo

MTSK, el modelo de Conocimiento Especializado del Profesor de Matemáticas.

Una breve reseña histórica del modelo

En 2013, en el 8º Congreso Europeo de Investigación en Educación Matemática, en Antalya, Turquía, el grupo de investigación en Didáctica de las Matemáticas de la Universidad de Huelva presentó una crítica al modelo Mathematical Knowledge for Teaching (MKT) desarrollado por Deborah Ball y sus colaboradores (vid. Flores et al., 2013). Dicha crítica, motivada por las dificultades analíticas que había mostrado en los estudios empíricos del SIDM, estaba centrada en la noción de especializado que se manejaba en el MKT y cuya contrapropuesta, presentada por Carrillo et al. (2013), mostraba una visión más general de tal noción. En Ball et al. (2008) se habla del conocimiento especializado del contenido como un conocimiento puramente matemático diferenciado del conocimiento común de las matemáticas propio de cualquier persona matemáticamente instruida. Eso, en sí mismo dificultaba el análisis a la hora de diferenciar entre común y especializado en diferentes países y niveles educativos; parecía más razonable pensar en la existencia de una forma especial de conocer las matemáticas por parte del profesor que implicaría no solo componentes matemáticas del conocimiento, sino también vinculadas a su consideración como objeto de enseñanza y aprendizaje. En el MTSK, la noción de especializado se establece como un conjunto de conocimientos que, en general, solo tienen sentido para el profesor de matemáticas, aunque en lo individual algunos conocimientos puedan ser compartidos con otros profesionales. Esta noción se relaciona con la especialización. Durante los siguientes 5 años, las investigaciones doctorales y posdoctorales, así como la colaboración con otros grupos de investigación y la discusión en foros académicos, ayudaron a que la propuesta del MTSK se consolidara y, como una sistematización de tales esfuerzos, en 2018 se publicó el artículo «The Mathematics Teacher’s Specialised Knowledge (MTSK) model» (Carrillo et al., 2018). Este artículo supuso la posibilidad de comunicar el modelo a público no hispanoparlante (cabe señalar que el modelo ya era ampliamente consultado por investigadores de lengua portuguesa y había sido discutido en foros en inglés, pero la publicación citada se destaca por su carácter de síntesis). En julio de 2020, el MTSK había logrado una diseminación importante, no solo entre lectores interesados en el tema, sino también entre investigadores comprometidos por realizar un trabajo colaborativo en torno del modelo. Es así como la Asociación Universitaria Iberoamericana de Postgrado (AUIP) reconoció al grupo de trabajo como una Red colaborativa con presencia en 11 países de la región.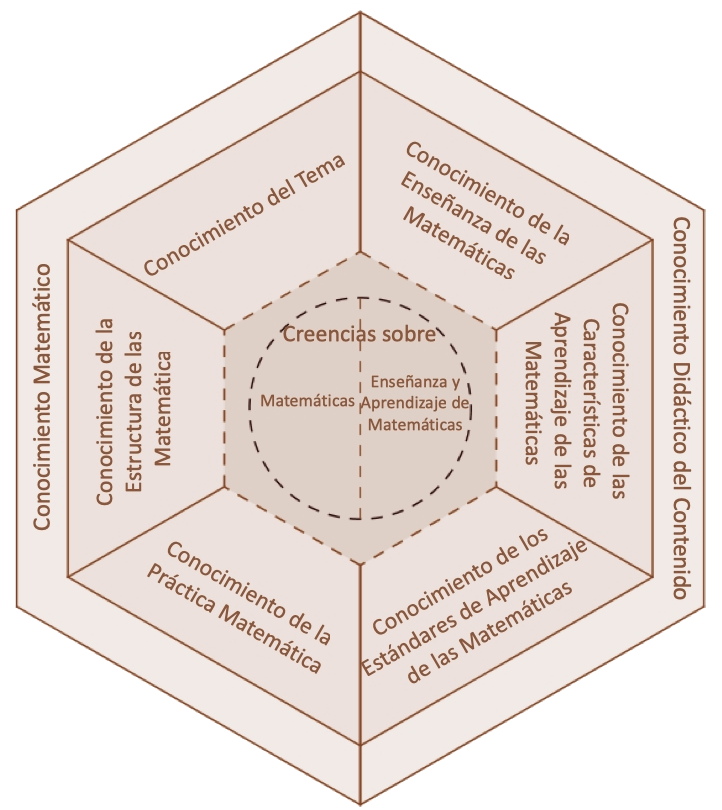

¿Qué es el MTSK?

El MTSK es un modelo con fines analíticos. Esto significa que, además de ser una propuesta que explica la composición de aquellos conocimientos que hacen del profesor un especialista de la enseñanza de las matemáticas, también es una herramienta que permite realizar análisis finos sobre tal tipo de conocimiento. Este modelo forma parte de aquellos que toman como base las ideas de Lee Shulman acerca del conocimiento profesional del profesor (e.g. Shulman, 1987). Se consideran tres grandes dominios en el MTSK, los cuales son el Dominio de Conocimiento Matemático, el Dominio de Conocimiento Didáctico del Contenido y el Dominio de las Creencias.

¿Cómo se constituye el MTSK?

Desde el punto de vista jerárquico, el modelo MTSK organiza su contenido en dominios, subdominios, categorías y descriptores e indicadores. Los tres dominios comprenden el conocimiento matemático, el conocimiento didáctico del contenido y las creencias. El Dominio de Conocimiento Matemático considera tres subdominios. El primero, el Conocimiento de los Temas, comprende un conocimiento sobre los objetos matemáticos y los procesos atribuibles a estos. Las categorías que lo componen son procedimientos; definiciones, propiedades y sus fundamentos; registros de representación, y fenomenología y aplicaciones. El segundo subdominio es el Conocimiento de la Estructura de las Matemáticas. En este, se considera el conocimiento que tiene el profesorado sobre la manera en la que se relacionan los objetos matemáticos. Sus categorías se conforman a partir de las conexiones de complejización, simplificación, transversales y auxiliares. Finalmente, el tercer subdominio es el Conocimiento de la Práctica Matemática y se conforma por los conocimientos sobre las formas de proceder y producir en matemáticas. La propuesta actual de categorías sitúa a cada práctica matemática (demostración, definición, ejemplificación, etc.) como una categoría. En el Dominio del Conocimiento Didáctico del Contenido también se consideran tres subdominios. Estos subdominios contemplan el conocimiento que tiene el profesorado sobre los objetos matemáticos como objetos de enseñanza, de aprendizaje y situados en un marco curricular. El Conocimiento de la Enseñanza de las Matemáticas contempla las categorías teorías de enseñanza; recursos materiales y virtuales, y estrategias, técnicas, tareas y ejemplos. El Conocimiento de las Características de Aprendizaje de las Matemáticas considera las categorías teorías de aprendizaje; fortalezas y dificultades; formas de interacción de los estudiantes con el contenido, e intereses y expectativas de los estudiantes frente a las matemáticas. Finalmente, el Conocimiento de los Estándares de Aprendizaje de las Matemáticas se conforma con las categorías aprendizajes esperados, nivel de desarrollo conceptual y procedimental esperado y la secuenciación de temas.

¿En qué niveles se ha empleado el MTSK?

Temáticas

• T1 Aplicaciones de MTSK en la formación de profesores

• T2 Investigaciones sobre el formador de profesores de matemáticas

• T3 MTSK en relación con distintos tópicos y etapas

• T4 Desarrollo del MTSK

• T5 Extensiones del MTSK

Publicaciones

En este espacio se encuentran las actas de los congresos de la Red que están publicadas, la referencia del artículo del 2018 que difunde en lengua inglesa una actualización del modelo MTSK y un listado de algunas publicaciones para iniciarse en el modelo.

Actas VI Congreso Iberoamericano sobre Conocimiento Especializado del Profesor de Matemática

2023 | R. Delgado-Rebolledo y D. Zakaryan (editoras) Publicado en: Pontificia Universidad Católica de Valparaíso Ver publicación

Actas IV Congreso Iberoamericano sobre Conocimiento Especializado del Profesor de Matemática

2020 | J. Carrillo, M. Codes y L. C. Contreras (editores) Publicado en: Universidad de Huelva Ver publicación

The mathematics teacher’s specialised knowledge (MTSK) model

2018 | José Carrillo-Yañez, Nuria Climent, Miguel Montes, Luis C. Contreras, Eric Flores-Medrano, Dinazar Escudero-Ávila, Diana Vasco, Nielka Rojas, Pablo Flores, Álvaro Aguilar-González, Miguel Ribeiro & M. Cinta Muñoz-Catalán Publicado en: Research in Mathematics Education, 20:3, 236-253, DOI: 10.1080/14794802.2018.1479981

Actas de las III Jornadas del Seminario de Investigación de Didáctica de la Matemática de la Universidad de Huelva

2017 | J. Carrillo y L. C. Contreras (editores) Publicado en: Universidad de Huelva

Actas de las II Jornadas del Seminario de Investigación de Didáctica de la Matemática de la Universidad de Huelva

2015 | J. Carrillo, L. C. Contreras y M. A. Montes (editores) Publicado en: Universidad de Huelva Ver publicación

Referencias

• Ball D.L., Thames, M.H., & Phelps, G. (2008). Content Knowledge for Teaching: What Makes it Special? Journal of Teacher Education, 59(5), 389-407.
• Carrillo, J., Climent, N., Contreras, L. C. y Muñoz-Catalán, M. C. (2013). Determining specialised knowledge for mathematics teaching. En B. Ubuz, C. Haser y M. A. Mariotti (Eds.). Proceedings of the CERME 8 (pp. 2985-2994). ERME.
• Carrillo, J., Climent, N., Montes, M., Contreras, L., Flores-Medrano, E., Escudero-Ávila, D. . . . Muñoz- Catalán, M. C. et al. (2018). The mathematics teacher’s specialised knowledge (MTSK) model. Research in Mathematics Education, 20, 236-253.
• Escudero-Avila, D. (2015). Una caracterización del conocimiento didáctico del contenido como parte del conocimiento especializado del profesor de matemáticas de secundaria [Tesis de doctorado]. Universidad de Huelva.
• Flores, E., Escudero, D. I. y Carrillo, J. (2013). A theoretical review of specialised content knowledge. En B. Ubuz, C. Haser y M. A. Mariotti (Eds.). Proceedings of the CERME 8 (pp. 2055-3064). ERME.
• Montes, M.Á., Contreras, L.C., Liñán, M.d.M., Muñoz Catalán, M.C., Climent, N. y Carrillo, J. (2015). Conocimiento de aritmética de futuros maestros. Debilidades y fortalezas. Revista de Educación, 367, 36-62.
• Montes, M., Pascual, M.I., y Climent, N. (2021). Un experimento de enseñanza en formación continua estructurado por el modelo MTSK. Relime, 24(1), 83-104.
• Ramírez-García, M., Joglar-Prieto, N., Muñoz-Catalán, M.C. (2018). Conocimiento especializado de una maestra de educación infantil en una tarea de descomposición numérica. En L.J. Rodríguez-Muñiz, L. Muñiz-Rodríguez, A. Aguilar-González, P. Alonso, F.J. García, A. Bruno (Eds.), Investigación en Educación Matemática XXII (p. 655). Universidad de Oviedo.
• Rojas, N., Flores, P., y Carrillo, J. (2015). Conocimiento Especializado de un Profesor de Matemáticas de Educación Primaria al Enseñar los Números Racionales. Bolema, 29(51), 143-166.
• Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22.
• Sosa, L., Flores-Medrano, E., y Carrillo, J. (2015). Conocimiento del profesor acerca de las características de aprendizaje del álgebra en bachillerato. Enseñanza de las Ciencias, 33(2), pp. 173-189.
• Vasco, D., Climent, N., Escudero-Ávila, D., Flores-Medrano, E. (2015). The characterisation of the specialised knowledge of a university lecturer in linear algebra. CERME 9 – Ninth Congress of the European Society for Research in Mathematics Education (pp.3283-3288). ERME